GRAPHS
A graph G can be defined as an ordered set G (V, E) where V (G) represents the finite and non-an empty set of vertices and E(G) represents the set of edges that are used to connect these vertices.
The graph is a non-linear data structure. It contains a set of points known as nodes and a set of links known as edges. Here edges are used to connect the vertices.
 |
| Graph G |
Example:
The following is a graph with 5 vertices and 6 edges.
This graph G can be defined as G = ( V, E )
Where V = {A, B, C,D, E} and E = {(A, B), (A, C)(A,D), (B,D), (C,D), (B, E), (E,D)}.
The following is a graph with 5 vertices and 6 edges.
This graph G can be defined as G = ( V, E )
Where V = {A, B, C,D, E} and E = {(A, B), (A, C)(A,D), (B,D), (C,D), (B, E), (E,D)}.
Graph terminologies:
Vertex: An individual data element of a graph is called Vertex. Vertex is also known as a node. In the above example graph, A, B, C, D & E are known as vertices.
Edge: An edge is a connecting link between two vertices. Edge is also known as Arc. An edge is represented as (starting Vertex, ending Vertex).In the above graph, the link between vertices A and B is represented as (A, B).
Adjacent Vertices: Two vertices u and v in an undirected graph G are called adjacent in G if u and v are endpoints of an edge e of G. Such an edge e is called the incident with the vertices u and v and e is said to connect u and v.
Degree of Vertex: The degree of a vertex in an undirected graph is the number of edges incident with it. A loop at a vertex contributes twice to the degree of that vertex. The degree of the vertex v is denoted by deg(v). A vertex of degree zero is called isolated. A vertex with degree one is called a pendant. Example: deg (A) = 3, deg (B) =3 deg (E)=2.
In-degree: The in-degree of a vertex v is the number of edges that are incoming - towards v (head of an edge). It is denoted by deg– (u).
Out-degree: the out-degree of a vertex v is the number of edges that are outgoing from v (tail of edge). It is denoted by deg+ (u).
Types of Graphs:
Directed Graph
In a directed graph, the connection between two nodes is one-directional.
It is a graph in which each edge has a direction to its successor. It is a graph with only directed edges.
 |
| Directed Graph |
Undirected Graph
In an undirected graph, all connections are bi-directional. It is a graph in which there is no direction on the edges. The flow between two vertices can go in either direction.
 |
| Undirected Graph |
Connected Graph
An undirected graph is called connected if there is a path between every pair of distinct vertices of the graph.
 |
| Connected Graph |
Not-Connected Graph
An undirected graph that is not connected is called disconnected.
 |
| Not-Connected Graph |
Strongly Connected Graph
A directed graph is strongly connected if there is a path from A to B and from B to A whenever A and B are vertices in the graph.
 |
| Strongly Connected Graph |
Weakly Connected Graph
A directed graph is weakly connected if there is a path between every two vertices in the underlying undirected graph. That is, a directed graph is weakly connected if and only if there is always a path between two vertices when the directions of the edges are disregarded.
 |
| Weakly Connected Graph |
Complete Graph
A graph in which any V node is adjacent to all other nodes present in the graph is known as a complete graph. An undirected graph contains the edges that are equal to edges = n(n − 1)/2 where n is the number of vertices present in the graph. The following figure shows a complete graph.
 |
| Connected Graph |
Regular Graph
It is the graph in which nodes are adjacent to each other, i.e., each node is accessible from any other node.
 |
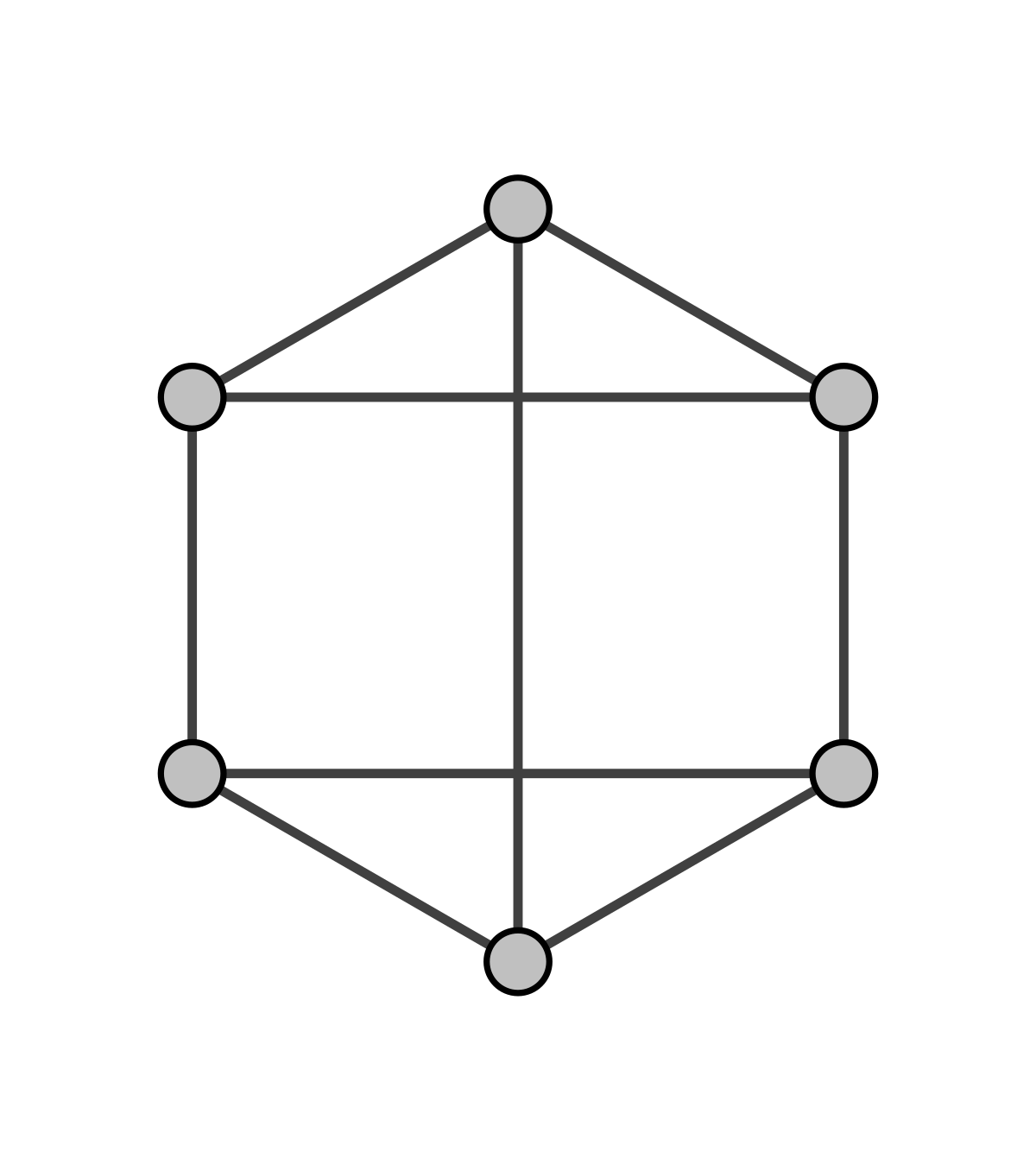| 3-o Regular Graph |
Cycle Graph
A graph having a cycle is called a cycle graph. In this case, the first and last nodes are the same. A closed simple path is a cycle.
 |
| Cyclic Graph |
Acyclic Graph
A graph without a cycle is called an acyclic graph.
 |
| Acyclic Graph |
Weighted Graph
Graphs that have a number assigned to each edge are called weighted graphs.
In a weighted graph, each edge has an associated numerical value, called the weight of the edge. Edge weights may represent distances, costs, etc. Example: In a flight route graph, the weight of an edge represents the distance in miles between the endpoint airports.
 |
| Weighted Graph |
Planar Graph
A graph is called planar if it can be drawn in the plane without any edges crossing, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints. In other words, it can be drawn in such a way that no edges cross each other.
 |
| Planar Graph |
Representation of Graphs:
1. Adjacency matrix
- We have a matrix of order n*n where n is the number of nodes in the graph.
- The matrix represents the mapping between various edges and vertices.
- In the matrix, each row and column represents a vertex. The values determine the presence of edges.
- Let Aij represents each element of the adjacency matrix. Then,
- For an undirected graph, the value of Aij is 1 if there exists an edge between i and j. Otherwise, the value of Aij is 0.
 |
| ADJACENCY MATRIX |
- For a directed graph, the value of Aij is 1 only if there is an edge from i to j i.e. i is the initial node and j is the terminal node.
 |
| ADJACENCY MATRIX |
- The time complexity of the adjacency matrix is O(n^2).
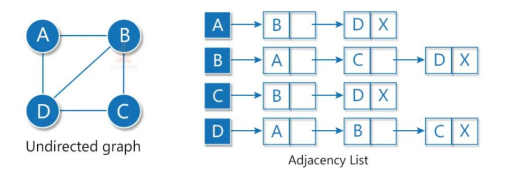
2. Adjacency list
- The adjacency list is an array of linked lists where the array denotes the total vertices and each linked list denotes the vertices connected to a particular node.
- In a linked list, the most important component is the pointer named ‘Head’ because this single pointer maintains the whole linked list. For linked list representation, we will have total pointers equal to the number of nodes in the graph.
- For an undirected graph, we will link all the edges in the list that are connected to a node as shown:
 |
| ADJACENCY LIST |
- In a directed graph, we will link only the initial nodes in the list as shown:
 |
| ADJACENCY LIST |
Applications of Graph
- In Computer science graphs are used to represent the flow of computation.
- Google maps use graphs for building transportation systems, where the intersection of two(or more) roads is considered to be a vertex, and the road connecting two vertices is considered to be an edge, thus their navigation system is based on the algorithm to calculate the shortest path between two vertices.
- Computer networks: Local area network, Internet, Web
- Facebook’s Friend suggestion algorithm uses graph theory. Facebook is an example of an undirected graph.
- In World Wide Web, web pages are considered to be the vertices. There is an edge from page u to another page v if there is a link to page v on page u. This is an example of a Directed graph. It was the basic idea behind Google Page Ranking Algorithm.