Huffman Coding Algorithm in 2022- Programmrs

 Huffman Algorithm

Huffman algorithm is a lossless data compression algorithm. It was developed by David Huffman. It is simply a technique for compressing data to reduce its size without losing any information.

Lots of compression systems use the Huffman algorithm for the compression of text, images, video, audio, data, etc. The general idea behind the Huffman algorithm is to use less number of bits to represent the most used keys.

For example:

Let's say we get four kinds of signals in the system.

     A     B      C     D

For such system, we might use 2 bit representation as:

A=00

B=01

C=10

D=11

Suppose we have data string as

AAABCAABBCDDAAAABAAABABABADDAAAABC

If the number of A is 10,000, B is 234, C is 45 and D is 134, then total storage required will be (10,000+234+45+134)*2 = 20,826 bits. According to Huffman, since A is repeated 10,000 times so space for it can be automatically reduced as a result total storage is also reduced.

While assigning the code word, the most frequently used symbol is assigned a codeword of length 1, and the final one gets a code word with all ones.

A=0

B=10

C=110

D=111

Now, for given data string the binary value will be

 00010110001010110111111000010000100100100111111000010110

• If we calculate the total bits required to store the data, it will be
• 10,000*1+ 234*2+45*3+134*3= 11,005 bits
• Total memory saved= 20,826- 11,005= 9,821 bits
• If the data to be stored is very large, then more bits will be saved.
• But the problem is how are going to recover the original data from the compressed string.

As a result, a tree is made according to the codeword assignment.

HUFFMAN TREE

Now, to decode the encoded string, read a bit at a time. Compare with a root node. If it is 0, then we are at the end decision point. So, it must be A. If it was 1, then we have to read the next bit again and check. If the next bit is 0 then it is B. Otherwise, read the next bit and check until we do not reach a decision point.

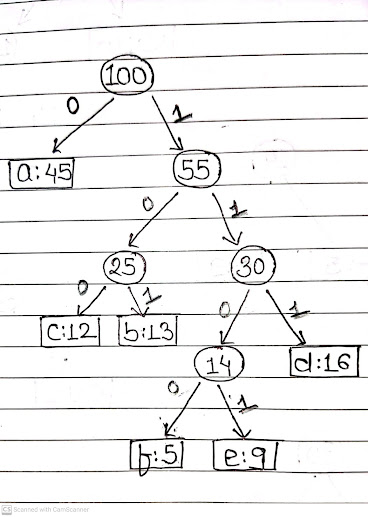
Construct a Huffman Code for the given Symbols.

Character	a	b	c	d	e	f
Frequency	45	13	12	16	9	5

Solution:

Arranging the frequencies in Ascending priority queue:

5

9

12

13

16

45

Note: Create a Tree with the two lowest priority frequencies

Step 1:

Arranging the frequencies in ascending priority queue

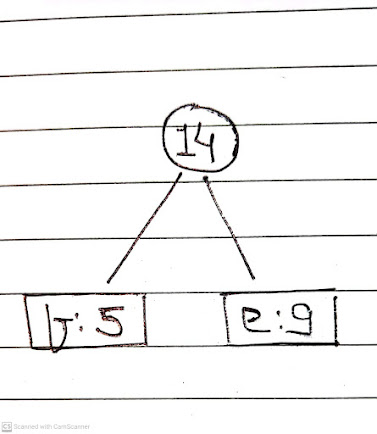
12

13

14

16

45

Step 2:

Arranging the frequencies in ascending priority queue

14

16

25

45

Step 3-

Arranging the frequencies in ascending priority queue

25

30

45

Step 4-

Arranging in ascending priority queue

45

55

Step 5-

FINALLY,

Applications of Huffman Algorithm:

• They are used for transmitting fax and text.
• They are used by conventional compression formats like PKZIP, GZIP, etc.
• Multimedia codecs like JPEG, PNG, and MP3 use Huffman encoding(to be more precise the prefix codes).